Timetabling

Theory

Burke, Kingston and de Werra gave a definition of timetabling.
A timetabling problem is a problem with four parameters:

• T, a finite set of times;
• R, a finite set of resources;
• M, a finite set of meetings; and
• C, a finite set of constraints.

The problem is to assign times and resources to the meetings so as to satisfy the constraints as far as possible.
See the next chapter, how these real objects are mapped to Java interfaces.

Literatur

Please see the link section.

Application Programming Interface

Introduction

Here you can download the class diagram of the important classes as low resolution png
Created with inkscape and gimp.
Generated from netbeans6.0m9: gstpl-mainModel.zip

Database Table

If you like the sql style you wil prefer this simplified image: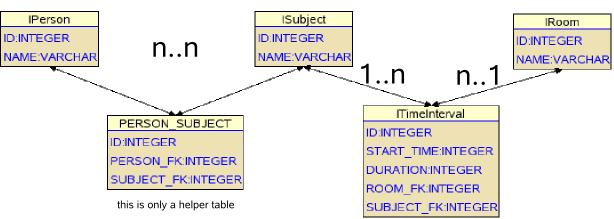

Basics

To be more precise we define some interfaces:

• IPerson, IRoom, ISubject and ITimeInterval.
• TimeAtom, which is not an extra class, see this file:TimeAtoms.png for a detailed description.

Relationship Table

To see how these classes are related to each other, see the following table:

Person1	Person2	...	PersonP		Subjects		Room1	Room2	...	RoomR
1	0		1		TimeInterval1 of Subject1		1	0		0
1	0		1		TimeInterval2 of Subject1		0	1		0
...			...		...
0	0		0		TimeIntervalJ of Subject2		0	1		0
					....
0	0		1		TimeIntervalT of SubjectS (SubjectS could have more TimeInterval's)		0	0		1

What you should see is the following:

1. One subject has one or more TimeInterval's that are the timeslots and define where and when the subject will take place.
2. person1 visits (at least) subject1.
3. personP visits (at least) subject1 and subjectS.
4. room1 is "occupied" at timeInterval1.
5. room2 is "occupied" at timeInterval2 and timeIntervalJ. Both should not collide, that means they shouldn't be at the same time or overlapp.
6. roomR is "occupied" at timeIntervalT.
7. subject1 takes place at timeInterval1 in room1 and timeInterval2 in room2 etc.
8. subject1 has - at least - person1 and personP as visitors

ITimeable

The ITimeable interface defines some basic operations, like retrieving all involved ITimeInterval's. An ITimeable has properties, too.
For example look at person1 in the previous table. If you call person1.getTIs() you get [ti1,ti2] - a list of ITimeInterval's.
Then you can e.g call ti1.getSubject() and you will get subject1.

ITimetable

A ITimeTable is a ITimeable with a root object.: e.g. one person has several ITimeInterval's, resulting from several ISubject's. So a person is the root and the ITimeInterval's are the leafs.
Possible ITimeTable's are: IRoom, ISubject, IPerson. So all basic classes are ITimetable except ITimeInterval - which is the leaf of the relation ship tree.
A ITimetable has a name.

ITimeInterval

A ITimeInterval (timeslot) is a ITimeable, too. But a TimeInterval is the 'leaf' from any Timeable 'tree' and it can exist even without a room and without a subject or both.
We cannot change the duration or the subject of a ITimeInterval implementation once it is created.
An ITimeInterval's-duration could only happen on one day. This could be a limitation for companies with night shift. But you can split the ITimeInterval into two.

IStepFunction

This interface helps us to find free ITimeInterval's in every ITimeTable implementation.
Image you have the timeatoms (e.g. one timeatom are 5 minutes) on the x axis and the collisions on the y axis.

Timetablematrix vs. TimeIntervalSet

In research papers you will find the timetable of a person as a matrix. E.g. person1 = [[1,2,3,1,4], [1,4,2,3,2]]. So in this example we have 2 days with 5 time slots and 4 subjects (1,2,3,4). In this application I haven't implement the TimeIntervalSet as a static matrix as showned above. It is more a thin matrix implementation. You can get the timetable of a person (TimeIntervalSet) with IWeekTimeIntervalSet person1.getWeekTISet(noOfWeek).

So as the name of IWeekTimeIntervalSet suggests, it is a set of ITimeInterval's which forms a week and you have several methods to handle this object. You can add and remove ITimeInterval's, count the gaps and collisions, transform it into a IStepFunction implementation and make a logical or(WeekTISet) or and(WeekTISet) operation. An 'or(WeekTISet)' operation is quite similar to an addAll(WeekTISet.getTimeIntervals) . But after you do an and(IWeekTISet) you will have one layer of ITimeInterval's resulting of the places with collisions.

When is the matrix implementation better?
It could be faster.
When is the thin matrix implementation better?
You can have time slots of different length and it saves memory if the user allows several time slots.

IAlgorithm

All algorithms implements the IAlgorithm interface. IAlgorithm offer some useful methods for computer controlled timetabling e.g.:

• 'AlgorithmObjects getObjects' returns the data, which is involved in the optimization process
• 'IAlgoProperties getProperties' returns the object which gives us control over this special algorithm object.

To handle several algorithms, which can be stacked I introduced AlgorithmObjects which has the following methods:

• 'GeneralAlgoProperties getProperties' returns the object which gives us the control over all involved algorithm. E.g. with that object we can adjust the maximal optimization time.
• List<IPerson> getPersons, returns a list of persons
• List<ISubject> getSubjects, returns a list of subjects
• etc.